Almost Alternating

A knot is called almost alternating if it has a diagram for which one crossing change results in an alternating diagram, but the knot is not alternating.

Specific Knots

The knot 820 is almost alternating. By changing the crossing indicated in the figure below, we obtain a diagram for an alternating knot.
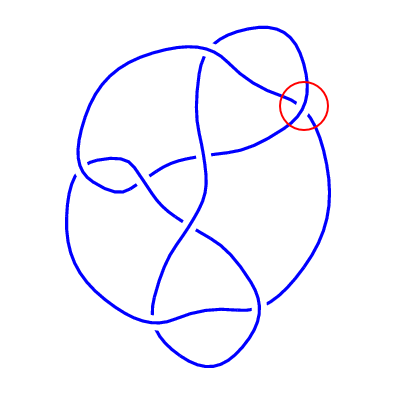crossing change making 8_20 alternating
820

11n95 is not almost alternating; see [2].

11n183 is almost alternating; see [3].

12n{242, 472, 574, 679, 688, 725, 888} are almost alternating. See [5].

References

[1] Adams, C. et. al., "Almost alternating links," Topology and it Apps. 46 (1992) 151-165.

[2] Dasbach, O. T. and Lowrance, A. M., "Invariants for Turaev genus one links", Comm. Anal. Geom. 26 (2018), 1101-1124.

[3] Goda, H., Hirasawa, M. and Yamamoto, R., "Almost alternating diagrams and fibered links in S^3", Proc. London Math. Soc. (3) 83 (2001) 472-492.

[4] Jablan, S., "Almost alternating knot with 12 crossings and Turaev Genus", Arxiv preprint.

[5] Truol, P., "The Upsilon invariant at 1 of 3-braid knots", Alg. and Geo. Top. 23 (2023) 3763-3804. Reprint. Arxiv preprint.

Privacy Notice