Arc Index

Page provided by Peter Cromwell, 4 April 2005.

Please see Thurston Bennequin page and Grid diagram page for a more recent information.

Definition

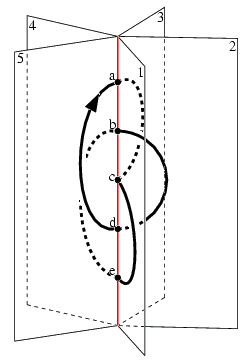
knot diagram

We give 3-space an open-book decomposition in which the z-axis is the binding and the pages are half-planes. An arc presentation of a link L is an embedding of L in finitely many pages of the open-book decomposition so that each of these pages meets L in a single simple arc.

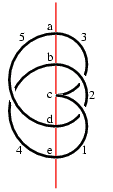
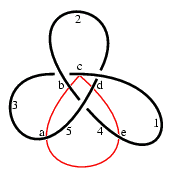
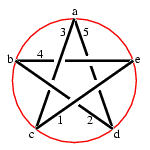
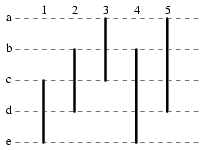
An arc presentation of the trefoil is shown on the right. The knot is embedded in five half-planes numbered 1 to 5 in sequence around the binding axis (shown in red); the knot meets the binding in five points, called vertices, labelled a to e in sequence along the axis.

It is important that the link meets each page in only one arc; if this restriction is removed, three pages always suffice for any link.

The minimum number of pages required to present a given link L in this manner is a link invariant called the arc index of L. It is denoted by the Greek letter α.

The information required to describe an arc presentation can be represented in many ways, some of which are shown below. This flexibility has led to its use in studying a wide variety of problems (see next section).

knot diagram knot diagram knot diagram grid form diagram
axial form annotated diagram layered chords grid form

Early Uses

Over the years, arc presentations have appeared in the literature several times in different guises:

In one of the earliest papers on knot theory, Hermann Brunn asked whether it was possible to have a projection of any link with a single singular point of high multiplicity. His solution was to construct something similar to an arc presentation and then look along the axis [6].

Lee Neuwirth used arc presentations to show the fundamental group of the link complement in which the relators do not contain inverse powers of the generators. He called them "asterisk presentations" [14].

A link diagram can be drawn so that all the lines are horizontal or vertical, and the over-crossing strands are always vertical. Such diagrams are similar to the grid form of an arc presentation. Herbert Lyon called them square-bridge presentations and used them in 3-manifold constructions. In this form, they are easily seen to be closely related to Legendrian links [11].

Lee Rudolph called them fences (the vertical lines being the posts and the horizontal ones the wires) in his study of quasipositivity [17].

link diagram Joan Birman and Bill Menasco discovered that the companion torus of some braided satellite links can be arranged as a tubular neighbourhood of an arc presentation of the companion knot.

The image on the right shows the construction of a braided bidirectional satellite. The vertical line is an axis that provides the reference frame for the structure. The transparent tube is the companion torus and is a tubular neighbourhood of an arc presentation of the trefoil having the green line as its axis. The two loops of the satellite run around the torus in opposite directions (a bidirectional satellite) but they run around the axis in the same direction (braided satellite) [5].

Recent Developments

In the cases above, arc presentations were used only as a tool in proofs. Arc index was first studied as an invariant in its own right in the early 1990s, after it was connected with the satellite construction.

Peter Cromwell showed that the invariant is well defined, found moves analogous to the Reidemeister or Markov moves for interconverting two arc presentations of the same link, investigated behaviour under distant union and connected sum, and found the arc index of 2-bridge links [7], [8].

Ian Nutt enumerated all knots with arc index at most 9. Elisabetta Beltrami showed that the remaining non-alternating 10 crossing knots have arc index 10 [3], [4], [16].

Hugh Morton and Elisabetta Beltrami showed that arc index is bounded below by the breadth of the Kauffman polynomial F(a,x) [13].

Yongju Bae and Chan-Young Park gave a construction that shows the arc index of a non-split link is at most the crossing number plus 2. Combined with the polynomial bound, this shows that the arc index of an alternating non-split link equals its crossing number plus 2 [1].

Arc presentations are closely related to Legendrian knots and links in contact structures. A simple deduction from work of John Etnyre and Ko Honda shows that the arc index of a (p,q) torus knot is p+q [9].

Recent connections with Heegaard Floer homology have prompted further study of the arc index. Of particular note is [15], in which values for 11 crossing nonalternating knots are determined. This work was done using computations by Baldwin and Gillam [2], and using also the program Gridlink,

The arc indices of all non-alternating 13 crossing knots were determined in the paper [18].

Please see Thurston Bennequin page and Grid diagram page for more recent information.

Specific Knots

12n_{41, 119, 120, 121, 145, 153, 199, 200, 243, 260, 282, 310, 322, 351, 362, 368, 377, 403, 414, 425, 475, 523, 549}
   Ref. [11]

References

[1] Bae, Y. and Park, C.-Y., An upper bound of arc index of links, Math. Proc. Cambridge Philos. Soc. 129 (2000), 491-500.

[2] Baldwin, J. and Gillam, W., "Computations of Heegaard-Floer knot homology." Arxiv preprint.

[3] Beltrami, E., Arc Index of Links, Ph.D. Thesis, Pisa University (1998).

[4] Beltrami, E., Arc index of non-alternating links, J. Knot Theory and Its Ramifications 11 (2002) 431-444.

[5] Birman, J. S. and Menasco, W. W., Special positions for essential tori in link complements, Topology 33 (1994) 525-556.

[6] Brunn, H., Uber verknotete Kurven, Verhandlungen des Internationalen Math. Kongresses (Zurich 1897), Leipzig, 1898, 256-259.

[7] Cromwell, P. R., Embedding knots and links in an open book I: basic properties, Topology and Its Applications 64 (1995), 37-58.

[8] Cromwell, P. R., Arc presentations of knots and links, Knot Theory (Proc. Conference Warsaw 1995), eds. V. F. R. Jones et al., Banach Center Publications 42 (1998), 57-64.

[9] Culler, M., Gridlink.

[10] Etnyre, J. B. and Honda, K., Knots and contact geometry I: torus knots and the figure eight knot, J. Symplectic Geometry 1 (2001) 63-120.

[11] Gyo Taek Jin et al., "Prime knots with arc index up to 10," Intelligence of low dimensional topology, Knots and Everything vol. 40 (2006), pp 65-74.

[12] Lyon, H. C., Torus knots in the complements of links and surfaces, Michigan Math. J. 27 (1980), 39-46.

[13] Morton, H. R. and Beltrami, E., "Arc index and the Kauffman polynomial," Math. Proc. Cambridge Philos. Soc. 123 (1998), 41-48.

[14] Neuwirth, L. P., Projections of knots, Algebraic and Differential Topology: Global Differential Geometry, ed. G. M. Rassias, Teubner-Texte zur Math. 70 (1984), 198-205.

[15] Ng, L., "On Arc index and maximal Thurston-Bennequin number." Arxiv preprint.

[16] Nutt, I. J., Braid Index of Satellite Links, Ph.D. Thesis, Liverpool University (1995).

[17] Rudolph, L., Quasipositive annuli (constructions of quasipositive knots and links IV), J. Knot Theory and Its Ramifications 4 (1992) 451-466.

[18] Hwa Jeong Lee, Yoonsang Lee, Chanmin Lee, Yeseo Park, Hun Kim, Gyo Taek Jin, Minimal grid diagrams of the prime knots with crossing number 13 and arc index 13. Arxiv preprint

Privacy Notice