Combinatorial definitions of polynomial invariants
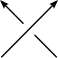
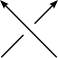
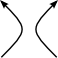
In the literature, several different conventions are used in the skein theoretic definitions of the polynomial invariants. We adopt the following for Jones, HOMFLY(PT), and Kauffman polynomials: denote the unknot by O and
L+ L- L0
| Variable(s) | Defining skein relation | |
| Jones polynomial V(L) | t | V(O) = 1, t-1 V(L+) - t V(L-) = (t1/2-t-1/2) V(L0) |
| HOMFLY(PT) polynomial P(L) | v, z | P(O) = 1, v-1 P(L+) - v P(L-) = z P(L0) |
| Kauffman polynomial F(L) | a, z | F(L)=a-w(L) Λ(D) where w(L) is the writhe
and Λ(O) = 1, Λ( 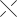 ) +
Λ( ) +
Λ(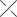 ) = z
(Λ( ) = z
(Λ(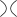 ) +
Λ( ) +
Λ(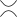 )), )), Λ( 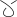 ) =
a Λ( ) =
a Λ( ),
Λ( ),
Λ(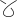 ) =
a-1 Λ( ) =
a-1 Λ( ) )
|
| The polynomials are related as follows: | V(t) | = | P(v←t, z←t1/2-t-1/2) |
| = | F(a←-t3/4, z←t1/4+t-1/4) |
Our conventions agree with those in [1].
The following table compares other conventions with ours. In most cases other conventions are either identical with ours, or those for the mirror image. "Same" and "Mirror" designates the former and the latter, respectively.
| Jones' Bull. AMS paper [2] |
F-Y-H-L-M-O's Bull. AMS paper [3] |
Kauffman's Trans. AMS paper [4] |
Bar Natan's KnotTheory [5] |
Wikipedia [6] | |
| Jones polynomial |
Mirror (t-1 is used in place of t) | Same | Same | ||
| HOMFLY(PT) polynomial |
ℓP(L+)+ℓ−1P(L-)=−mP(L0) xP(L+)+y−1P(L-)=−zP(L0) |
Mirror (a-1 is used in place of v) | Mirror (α-1 is used in place of v) | ||
| Kauffman polynomial |
Same | Same | Same | ||
References
[1] Kawauchi, A., A survey of knot theory, Birkhauser Verlag, Basel, 1996. xxii+420 pp.[2] Jones, V., A polynomial invariant for knots via von Neumann algebras, Bull. Amer. Math. Soc. (N.S.) 12 (1985), no. 1, 103--111.
[3] Freyd, P.; Yetter, D.; Hoste, J.; Lickorish, W. B. R.; Millett, K.; Ocneanu, A., A new polynomial invariant of knots and links, Bull. Amer. Math. Soc. (N.S.) 12 (1985), no. 2, 239-246.
[4] Kauffman, L. H., An invariant of regular isotopy, Trans. Amer. Math. Soc. 318 (1990), no. 2, 417-471.
[5] Bar-Natan, D., The Mathematica Package KnotTheory`, http://katlas.math.toronto.edu/wiki/The_Mathematica_Package_KnotTheory%60
[6] Wikipedia, The Free Encyclopedia, retrived August 19, 2009.