Monodromy
Page provided by Mark Bell, Warwick Mathematics Institute.
The complement of a fibered knot is the total space of a fiber bundle over S1. These are determined by a monodromy h, an element of the mapping class group of the fiber surface S such that the complement is:
where (x, 1) ~ (h(x), 0).
To represent such a monodromy, we fix the following curves on the surfaces with one puncture and genus one through five.

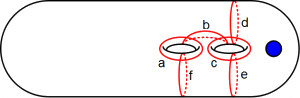
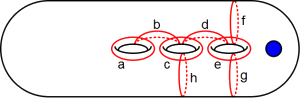
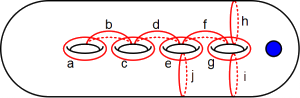

In each case, the Dehn twists about these curves generate the surface's mapping class group. Thus we encode a mapping class as a word in the letters aAbBcCdDeEfFgGhHiIjJkKlL, where x denotes a right Dehn twist about x and X denotes a left Dehn twist about x. Letters act on the left so when a word is read from left to right it agrees with the order of composition. For example aaabbC acts as a(a(a(b(b(C(.)))))).
The initial set of monodromy data for hyperbolic, fibered knots was produced using Twister and SnapPy. For the surface of genus g, all words with length at most L(g) were considered. These words were ordered short lexicographically according to the ordering: a < A < b < B < … < l < L. This ordering was chosen for computational reasons. Thus if a monodromy of a hyperbolic, fibered knot of genus g is provided, it is the short-lex first representative; if not, any representation of it must have length strictly greater than L(g).
| g | 1 | 2 | 3 | 4 | 5 |
| L(g) | 2 | 10 | 14 | 14 | 14 |