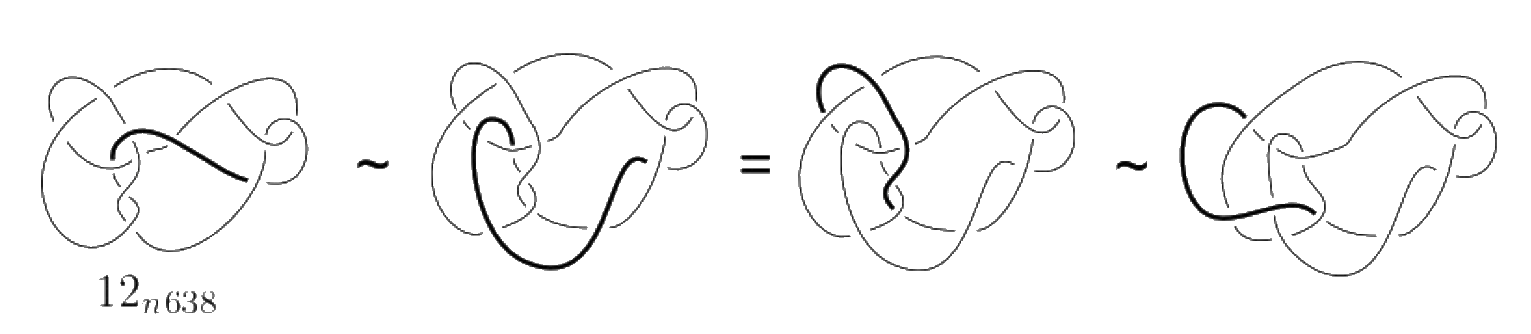Positivity
There are four notions of positivity presented in KnotInfo. In the table we enter Y, N, or Unknown if a knot
satisfies the condition on positivity.
If a (strongly)(quasi)positive braid is marked with a letter M, it means that the braid
represents the negative of the knot illustrated. The PD notation and braid notation match the figure.
Positive Braids: A knot is called a positive braid knot if it can be represented as the closure of a positive braid.
Positive Knots: A knot is called positive if it has a diagram in which all crossings are positive.
Strongly Quasipositive: A braid is called strongly quasipositive if it is the product of conjugates of
positive generators of the braid group ( σi), where each conjugating element is of the form
(σj σ{j+1} . . . σ{i-1}).
A knot is called strongly quasipositive if it is the closure of a strongly quasipositive braid.
(Strictly) Almost Strongly Quasipositive: A braid is called (strictly) almost strongly quasipositive if it is the product of conjugates of canonical generators σj±1 of the braid group, where each conjugating element is of the form (σj σj+1 ... σi-1), such that the number of negative generators used is exactly one. A knot is called (strictly) almost strongly quasipositive if it is the closure of a (strictly) almost strongly quasipositive braid.
In general, almost strongly quasipositive braids require at most one negative band. Thus, the set of strongly quasipositive braids is contained in the set of almost strongly quasipositive braids. We restrict ourselves to strictly almost strongly quasipositive braids for simplicity.
Initial data through 12 crossings was provided by Rebecca Sorsen; see references [4, 16].
Quasipositive: A braid is called quasipositive if it is the product of conjugates of positive
generators of the braid group ( σi). A knot is called quasipositive if it is the closure of a
quasipositive braid.
Each of these classes of knots is contained in the next. The only nontrivial inclusion follows from the
result that a positive knot is strongly quasipositive, a fact that follows from results of [11] and [12].
The main obstructions used to rule out possible positive representations of a knot are the following:
(1) If K is positive then its Conway polynomial has all coefficients nonnegative. See [4?].
(2) If K is positive, let h(P) be the highest degree coefficient of Homfly; this coefficient is
a polynomial in v. Then coefficients of h(P) are all nonnegative or all nonpositive. This is a result of Trackyz, quoted in [4?].
(3) If K is positive then twice the 3-genus is equal to the maximum z exponent in the Homfly polynomial,
which also equals the minimum v exponent in the Homfly polynomial [4?].
(4) Positive braids are fibered [9?].
(5) For a positive braid, t-g * Jones = 1 + t2 + kt3 + (higher order terms), where -1 ≤ k ≤ 3*(2g-1)/2 =
3g -3/2, where g is the three-genus. Note, this implies that -1 ≤ k ≤ 3g-2; see [10]. Results concerning the coefficients of the Homfly polynomial of positive braids can be found in [14].
(6) For a strongly quasipositive knot, the 4-genus equals the 3-genus. (This was proved by Rudolph.)
(7) For a quasipositive knot, twice the 4-genus is less than or equal to the minimum v degree in the Homfly polynomial [1].
Further references concerning positivity and Heegaard Floer homology include [4] and [6?].
Also, the positive notations for 12n638 was found by T. Abe, K. Tagami, and K. Moroi.
The positive notaton for 11n183 was found in [8?].
In the tables, if a knot has any particular positivity property, if an explicit representative is available, we include it. In [4], Hamer, Ito, and Kawamuro provide tools to find such representatives for strong quasi-positivity. Examples a listed below.
Specific Knots
10132
Stoimenow proved that this knot isn't quasipositive by considering its (2,0) cable. See [8?].
11n183
Stoimenow showed that this knot is positive in [9?].
12n638
Kenji Tagami and Tetsuyan Abe proved that this knot is positive. Here is a picture:
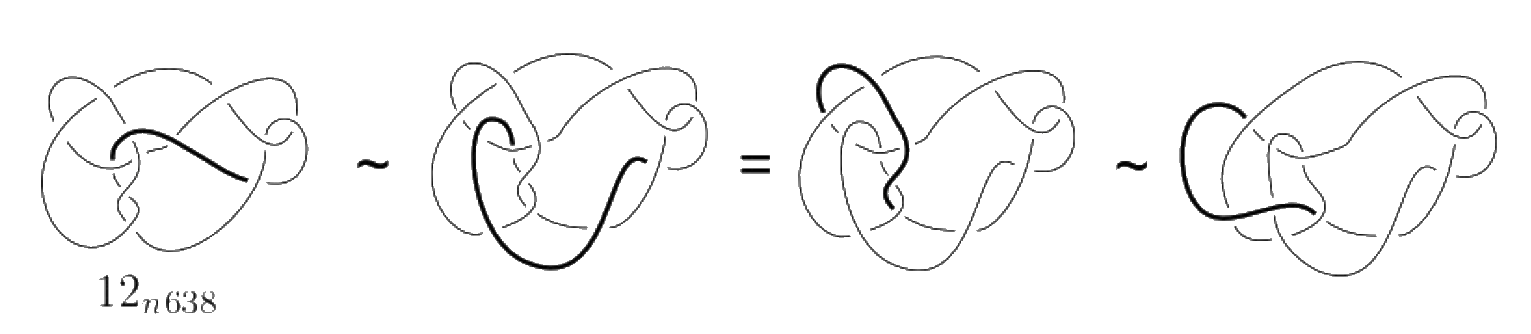
This was also proved independently by Katsumi Moroi.
{820, 821, 945, 946, 10126, 10127, 10131,
10133, 10140, 10143, 10145, 10148, 10149, 10155,
10157, 10159, 10165}
Sebastian Baader demonstrated the quasipositivity of these knots and found explicit descriptions of each as quasipositive
braids [1].
10145, 12n276, 12n329, and 12n402
Ken Baker has assisted us in identifying these and other knots as strongly quasipositive.
12n0113, 12n0114, 12n0190, 12n0191, 12n0233, 12n0234,
12n0344, 12n0345, 12n0466, 12n0467, 12n0570, 12n0604,
12n0666, 12n0674, 12n0683, 12n0684, 12n0707, 12n0708,
12n0721, 12n0722, 12n0747, 12n0748, 12n0767, 12n0820,
12n0822, 12n0829, 12n0831, 12n0882, 12n0887
Paolo Lisca has identified all of these knots as quasipositive. These follow from Theorem 2.1 from [6].
12n750
Peter Feller identified this knot as strongly quasipositive.
12n340
Lukas Lewark showed that this knot is not quasipositive, because the original Rasmussen invariant
and the generalised sl3-Rasmussen invariant are different for that knot, and these invariants agree on all quasipositive
knots [5].
11n17, 11n91, 11n99, 11n113,
11n162, 12n171, 12n176, 12n247, 12n270, 12n383,
12n441, 12n496, 12n520, 12n564, 12n626, 12n698,
12n699, 12n700, 12n701, 12n726, 12n734, 12n735,
12n796, 12n797, 12n814, 12n863, and 12n867.
Steve Boyer, Cameron Gordon, and Michel Boileau obstruct strong quasipositivity for these knots in [2].
Mikami Hirasawa provided the strongly quasipositive braid notation for 10a145, 12n276,
12n329, and 12n402.
Jesse Hamer, Tetsuya Ito and Keiko Kawamuro [4] have found strongly quasipositive braid notation for
12n_{148,149,293,321,332,366,404,432,528,642,660,801,830}.
12n148, 12n276, 12n329, 12n366,
12n402, 12n528, 12n660.
Lizzie Buchanan proves these are not positive in [15]. These knots were also resolved by Stoimenow.
10131, 10133, 10155
Stepan Orevkov found compact representations of these knots as quasipositive braids.
References
[1] Baader, S., "Slice and Gordian numbers of track knots," Osaka J. Math. 42, no. 1 (2005), 257-271.
[2] Boileau, M., Boyer, S., and Gordon, C., "Branched covers of quasipositive links and L-spaces," Arxiv preprint.
[3] Cromwell, P. R., "Homogeneous links," J. London Math. Soc. (2) 39 (1989), 535-552.
[4] Hammer, J., Ito, T., and Kawamuro, K., "Positivities of Knots and Links and the Defect of Bennequin Inequality," Experimental Mathematics, published online 29 April, 2019.
[5] Hedden, M., "Notions of positivity and the Ozsvath-Szabo concordance invariant," J. Knot Theory Ramification 19
(2010), 617-629.
[6] Lewark, L., http://lewark.de/lukas/foamho.html and
"sl3-foam homology calculations," Arxiv preprint.
[7] Lisca, P., "Stein fillable contact 3-manifolds and positive open books of genus one," Algebraic and Geometric
Topology 14 (2014), 2411-2430.
[8] Livingston, C., "Computations of the Ozsvath-Szabo knot concordance invariant," Goem. Topol. 8 (2004), 735-742.
[9] Stallings, J., "Constructions of fibred knots and links," Algebraic and geometric topology,
Proceedings of Symposia in Pure Mathematics 32 (American Mathematical Society, Providence, 1978) 55-60.
[10] Stoimenow, A., "On polynomials and surfaces of variously positive links," J. Eur. Math. Soc. (JEMS) 7 (2005), 477-509.
[11] Stoimenow, A., "On the crossing number of positive knots and braids and braid index criteria of Jones and
Morton-Williams-Franks," Trans. Amer. Math. Soc. 354(10) (2002), 3927-3954.
[12] Vogel, P., "Representations of links by braids," Com. Math. Helv. 65 (1990), 104-113.
[13] Yamada, S., "The minimal number of Seifert circles equals the braid index," Inv. Math. 88 (1987), 347-356.
[14] Ito, Tetsuya, "A note on HOMFLY polynomial of positive braid links," Arxiv preprint.
[15] Buchanan, Lizzie, "A new condition on the Jones polynomial of a fibered positive link" arxiv preprint.
[16] Capovilla-Searle, M., Kawamuro, K., and Sorsen, R., "Birman-Ko-Lee Left Canonical Form and its Applications," Arxiv preprint.
Privacy Notice