Gabai Width

(IN PROGRESS: Changing from "width" to "Gabai width." Data and text have not been updated yet.)

For a generic embedding of a knot K in R^3, the height function is Morse, having distinct critical values t_1< . . . < t_{2n}. The minimum value of n over all generic representatives of a knot K is the bridge index.

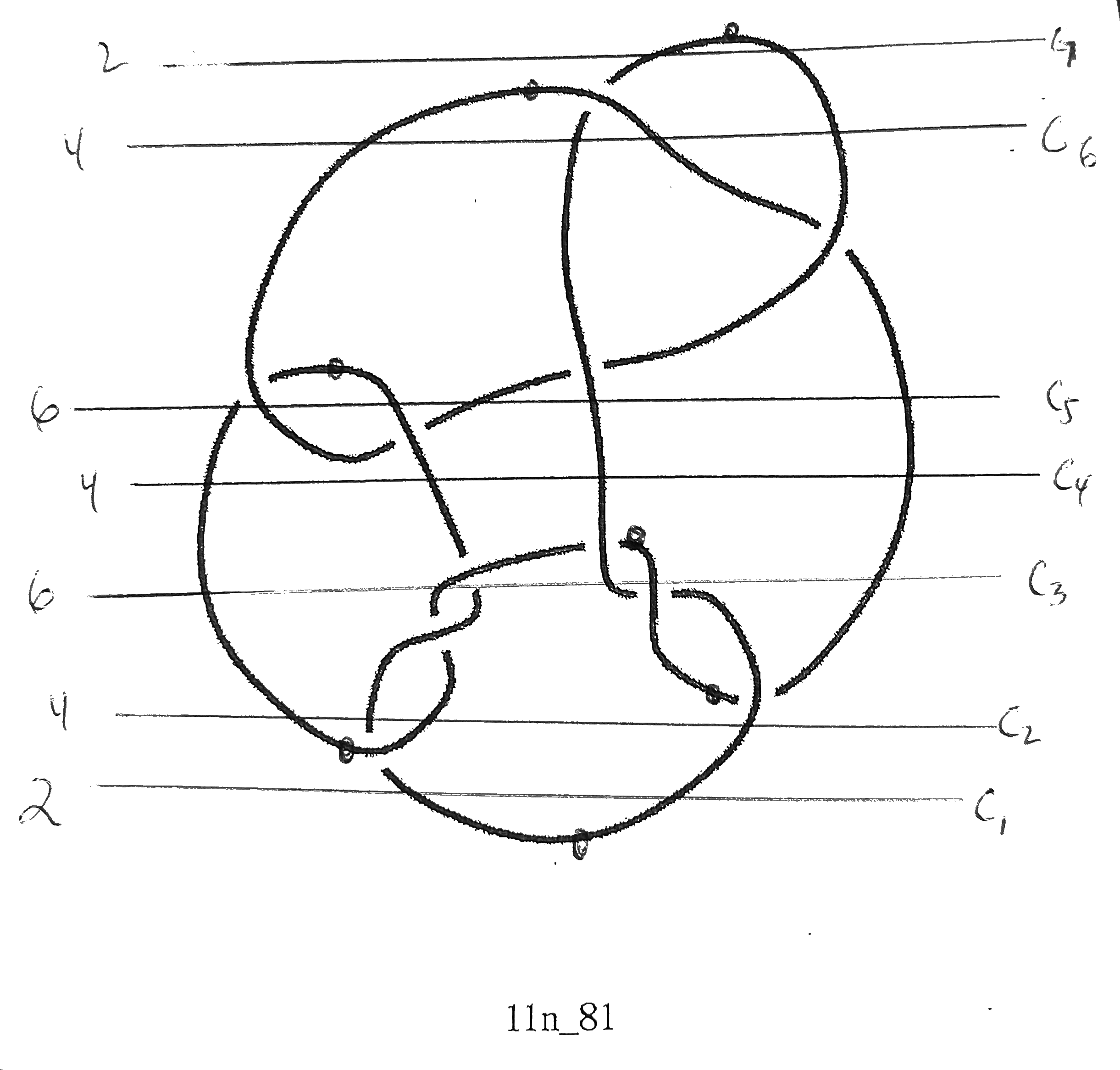
Choosing x_i, with t_i < x_i < t_{i+1}, for 0 < i < 2n, let c_i be the number of points on K at height x_i. The width of K, w(K), is the minimum value of the sum of the c_i, taken over all generic embeddings of K. This was defined by Gabai. (See the illustration below for an example.)

For 2-bridge knots, w(K) = 8. For a prime 3-bridge knot, w(K) = 18. For a prime 4-bridge knot in minimal position, there are two possibilities for the sequence of c_i: (2,4,6,8,6,4,2), in which case w(K) = 32, or (2,4,6,4,6,4,2), in which case w(K) = 28.

It is clear that the width satisfies subadditivity: w(K#J) <= w(K) + w(J) -2. Blair and Tomova provided examples for which the inequality can be strict.

An alternative (inequivalent) definition of width. (This definition, which we now denote w*(K), provides a useful measure of the complexity of certain algorithms that compute such invariants as the Khovanov homology of a knot.)

A generic embedding of K determines a sequence of c_i as described above. The "width" of that embedding could be defined as the maximum of the c_i. The alternative definition of the width is the minimum of this value, taken over all isotopic generic embeddings. We denote this w*(K). From the discussion, it is clear that for prime knots:

Br(K) = 2 implies w*(K) = 4 and w(K) = 8
Br(K) = 3 implies w*(K) = 6 and w(K) = 18
Br(K) = 4 and w*(K) = 6 implies w(K) = 28
Br(K) = 4 implies w*(K) = 8 and w(K) = 32

Of the 801 prime knots of 11 or fewer crossings, 186 are two-bridge and 600 are three-bridge. The remaining knots are 4-bridge knots: 11a_43, 11a_44, 11a_47, 11a_57, 11a_231 11a_263, 11n_71, 11n_72, 11n_73, 11n_74, 11n_75, 11n_76, 11n_77, 11n_78, 11n_81. All can be seen to be of width 4 by inspection. (11a263?)